Extracting Incentives from Black-Box Decisions

This week I’m headed to NeurIPS for the first time to present a workshop paper by me and Billy Moses.

The paper is about incentives in machine learning!

Incentives in Machine Learning?

Every algorithmic decision-maker incentivizes people to act in certain ways to receive better decisions. These incentives can dramatcally influence subjects’ behaviors and lives, and it is important that both decision-makers and decision-recipients have clarity on which actions are incentivized by the chosen model.

For example, when people know that their credit score will be partially determined by the number of credit cards they have, they’ll open more credit cards to get a better credit score. More grimly, imagine a child maltreatment predictor like the one used by Alleghany County. Much of the data used for prediction are from usage of public services, like food stamps. If usage of food stamps is caused by poverty, and poverty correlates with a higher risk of child maltreatment (e.g. because of the precarity of a weaker safety net) an ML-based decision-maker may learn to predict child maltreatment based on usage of food stamps. When deployed, it will incentivize parents to avoid crucial welfare, for fear their child will be taken away.

There are a number of concrete reasons to pay close attention to algorithmic incentives:

• They are sometimes legally regulated (e.g. adverse action notices in credit scoring require disclosure of which factors would change a decision).
• When disclosed, they empower individuals to have control and agency over their own outcomes.
• Whether we study them or not, all algorithms already incentivize behaviors, and are having unobserved consequences for decision-makers and decision-recipients in the real world.

Intuitively, for linear decision-making functions like logistic regression, figuring out the incentivized behaviors from the weights of the model is pretty straitforward: if the parameter \(w_i\) multiplying input feature \(x_i\) is positive, you’re incentivized to increase that feature (assuming you want to maximize your decision), and if negative you should decrease it. Similarly, the more positive a weight, the more you are incentivized to increase that feature (relative to other still-positively-incentivized features).

Unfortunately, this intuition breaks down when dealing with non-linear functions like neural networks. For example, consider a person (the gold diamond) trying to maximize their decision (blue line) by taking steps left or right.

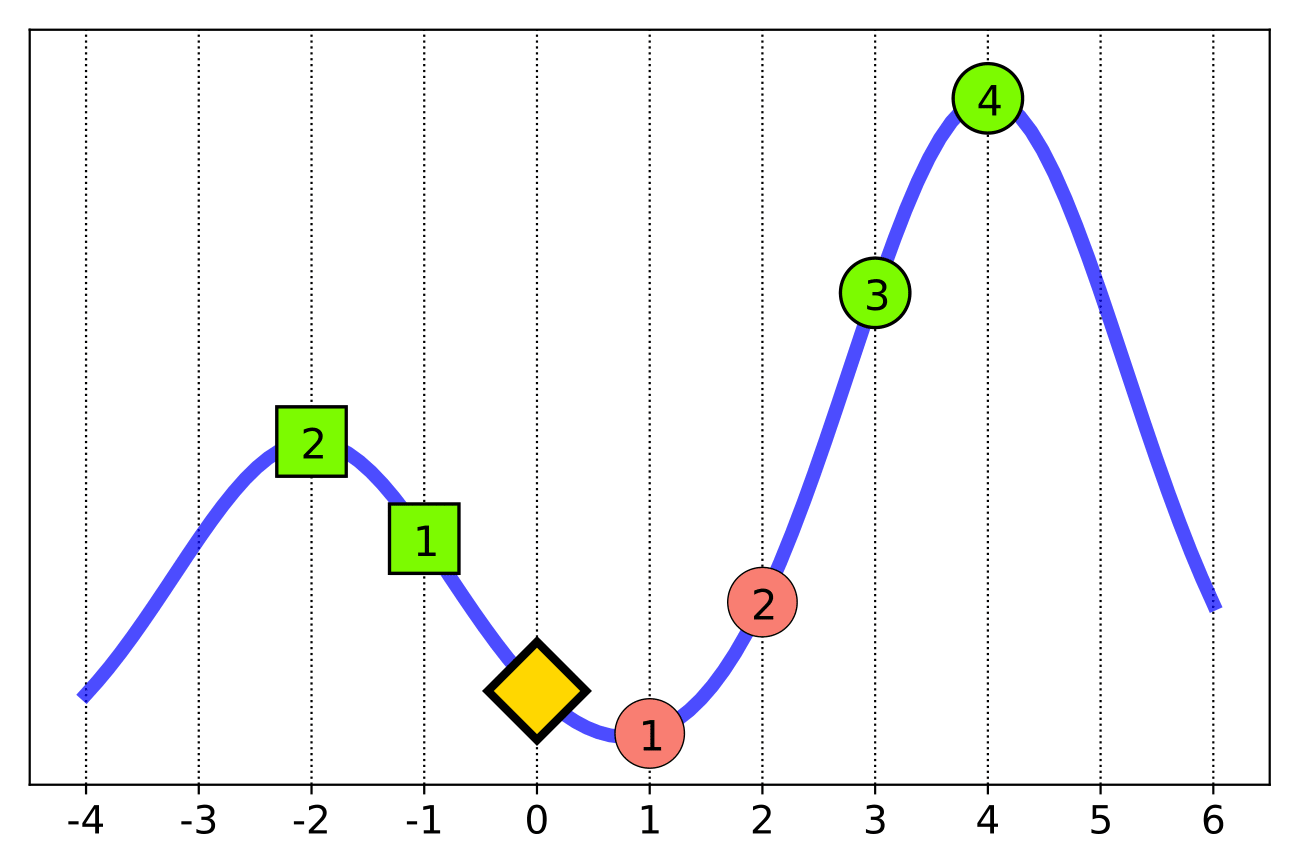
So, as the person, do you step left or right?

We might intuitively suppose we could simply look at the function’s local behavior and act based on that. These are the standard techniques employed by popular interpretability methods like LIME. But as the figure makes clear, pursuing the locally-incentivized behavior can actually lead to a highly suboptimal outcome over time.

One might imagine that restricting the function to be monotonic would solve this particular problem, as then even following local behavior would move us in the right direction. Unfortunately, even monotonic functions provide suboptimal incentives, as is demonstrated by an agent in the figure below (brighter colors mean a better decision).

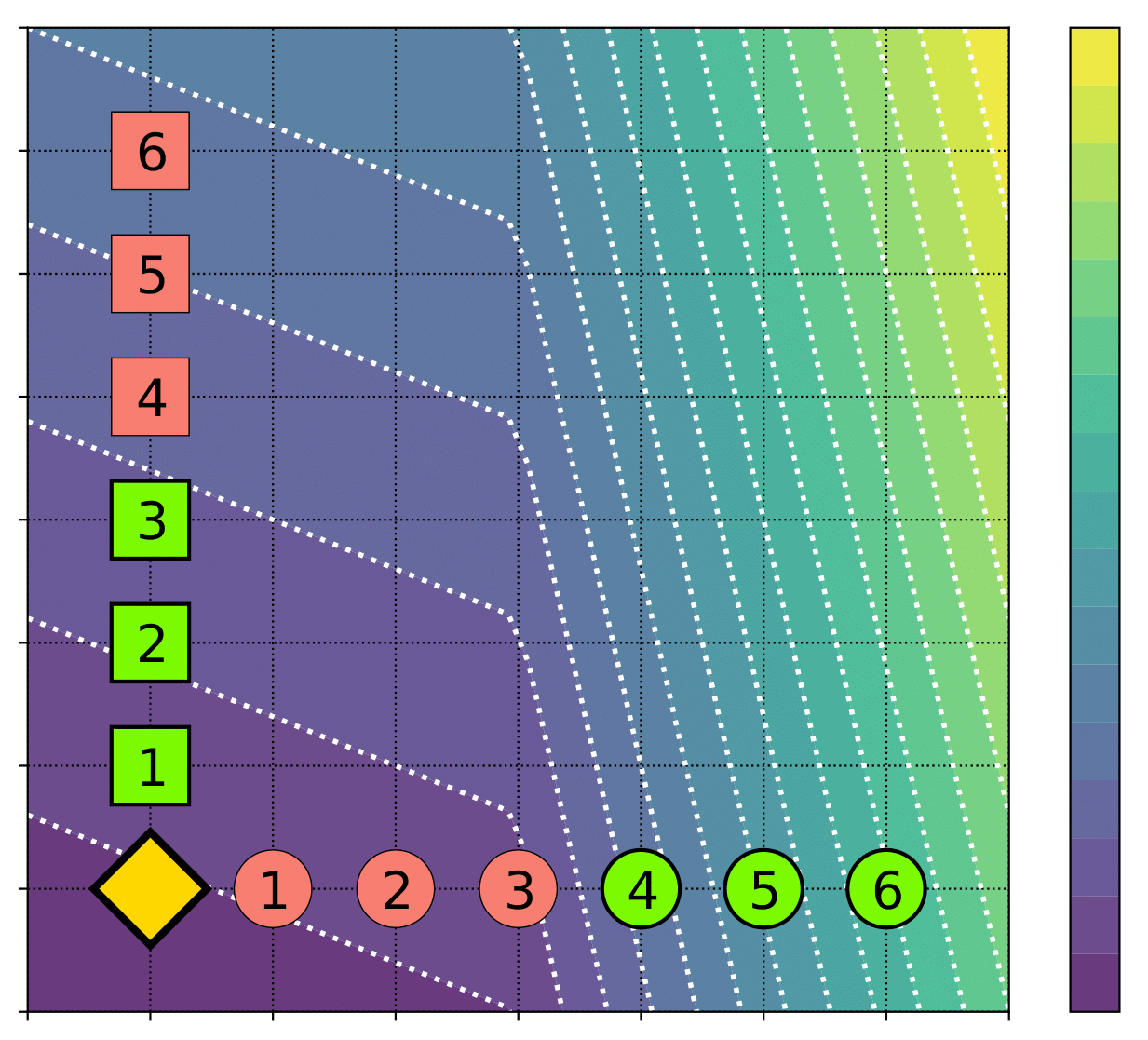
So, what do we do? Ideally, we’d like to understand how an algorithm incentivizes an individual to behave, such that they would maximize their long-term outcome.

One important observation is that, in both the 1-D and 2-D examples, which behavior was optimal at the moment depended on how many more steps you’d get to take before receiving the decision. Ideally, assuming you had \(k\) remaining actions, you’d look at every possible sequence of \(k\) actions and pick the best one. This would of course take exponential time.

Luckily, you can make this search much more efficient, through reinforcement learning!

Markov Decision Processes

The key insight of our paper is that agents subject to a decision-making function can be modeled as a Markov Decision Process, where the state is the current input feature vector, the actions are those actions available to the individual, and the reward at the final time-step the output of the decision-making function at the feature-values the agent ended at (and 0 at every other timestep).

By using well-studied reinforcement learning and planning methods (in experiments we used Monte-Carlo Tree Search) we can then approximate the optimal policy of this MDP. The actions recommended by such an MDP are the ones that will, if followed, lead to the best eventual decision, and are thus the most highly incentivized.

Note that this framework allows us to incorporate complex actions (which can be stochastic, can affect multiple features, and can even be state-dependent). Moreover, this framework doesn’t actually require any knowledge of the decision-making function other than having query access. This means that it can be used on complicated nonlinear functions (neural networks), non-differentiable functions (random forests), or even to audit proprietary decision functions we can’t access!

Most importantly, it allows us to find the maximally-incentivized actions: if we run it on our 1D example, it will tell us to step left if we have 2 or fewer actions, or right if we have 3 or more. Hooray!

The question remains, however: how well does this method work on practical, high-dimensional, highly-nonlinear real world decision-making functions?

Experiments

We looked at two domains: a violent recidivism predictor trained on the COMPAS dataset, and a free FICO credit scoring API to which we entirely lacked access.

Our results in both settings showed our algorithm improving over local explanations in real-world settings across the board.

(For risk scores, lower is better.) 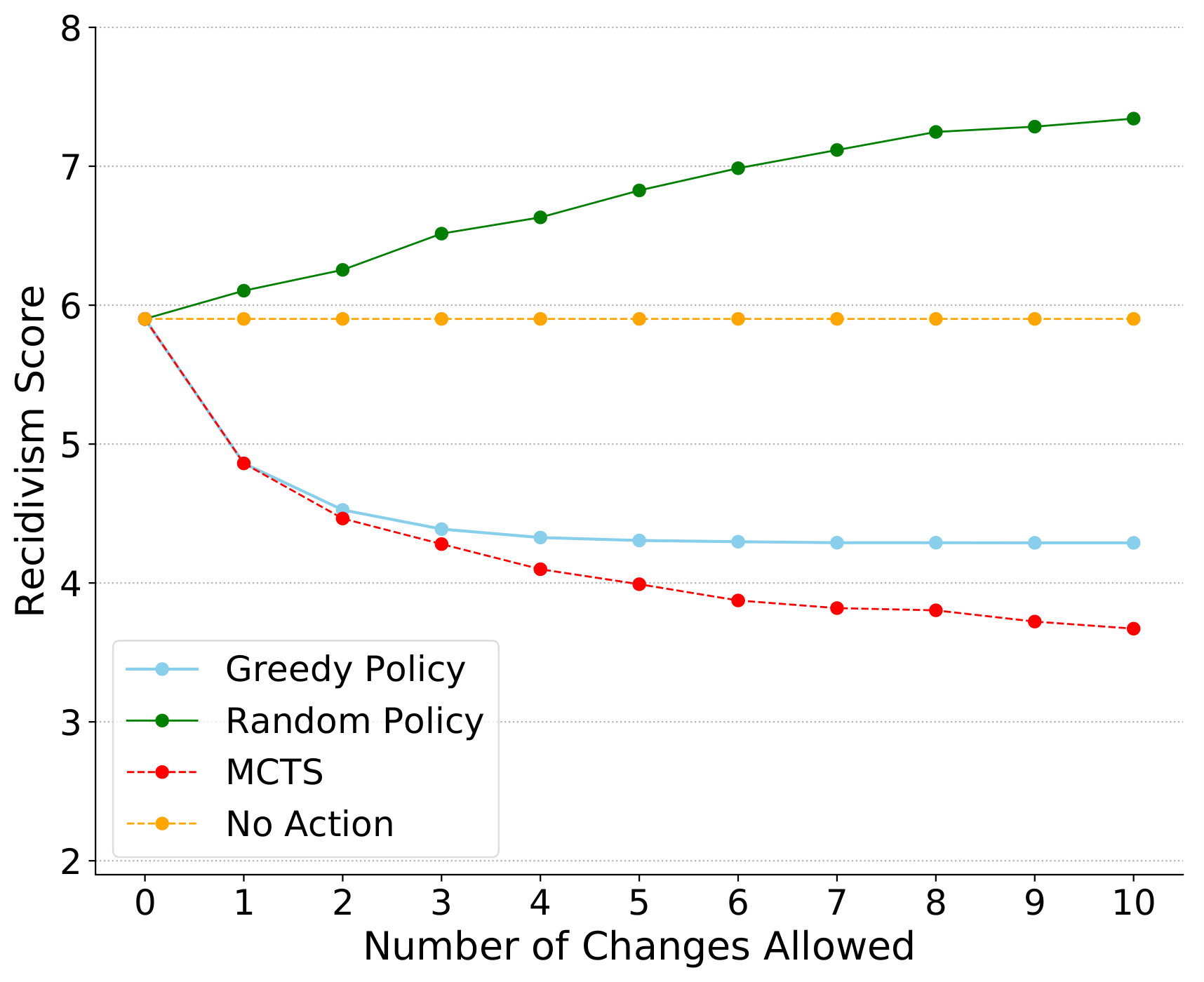(For credit scores, higher is better.)

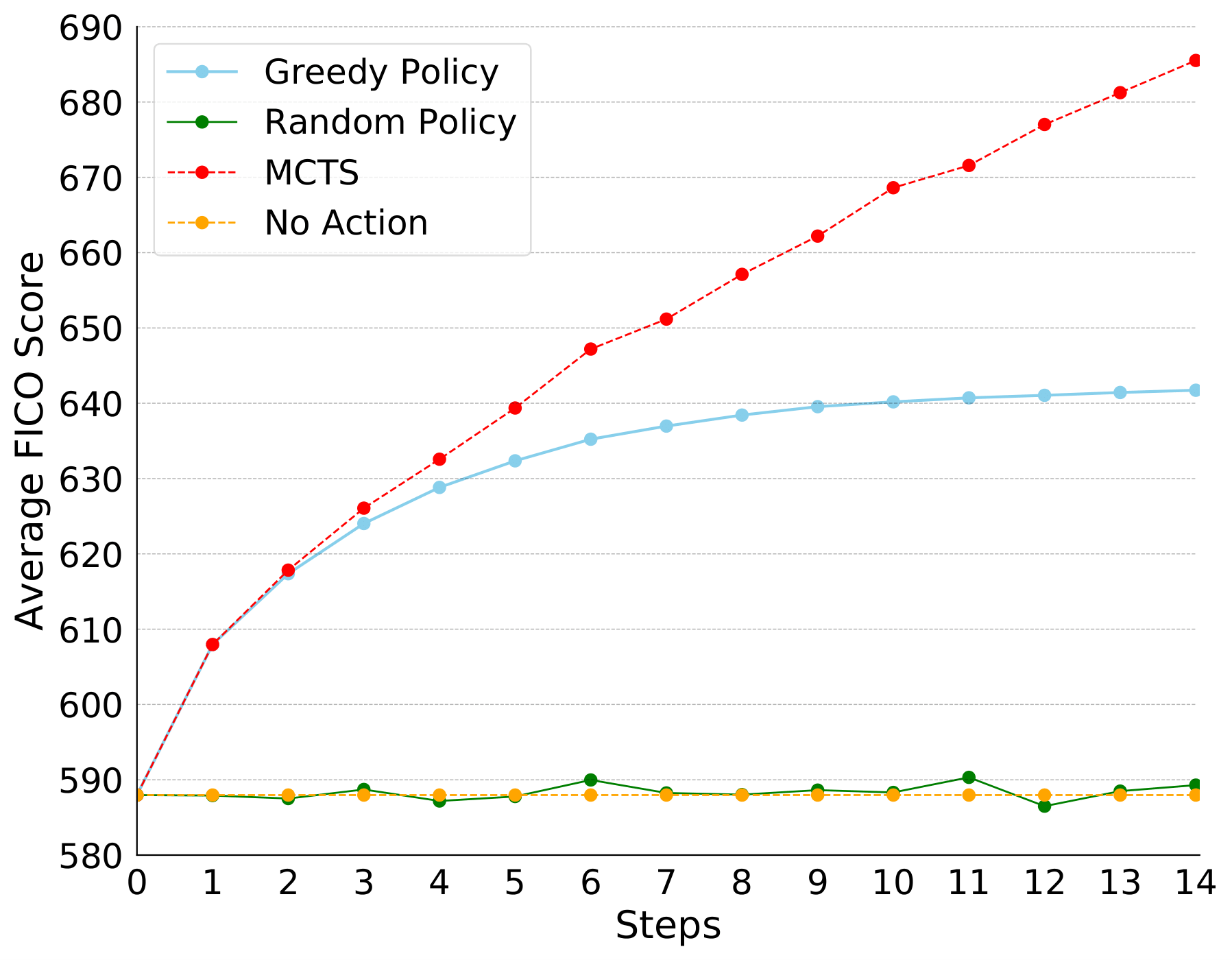
This is to be expected, but it’s still significant that we see the nonlinearity of real-world decision-making functions leading local approximations (marked as ‘greedy’ agents) astray. Thankfully, the MDP-based method appears to far outperform classical interpretability techniques on the problem of incentive generation.

For a more complete set of experimental results, along with lots more discussion about the nature of identifying ML incentives, you can see our paper. As a final thought, I’d like to highlight the results of one of our experiments, on the incentivization difference between a recidivism predictor that includes race and gender, vs. one that did not.

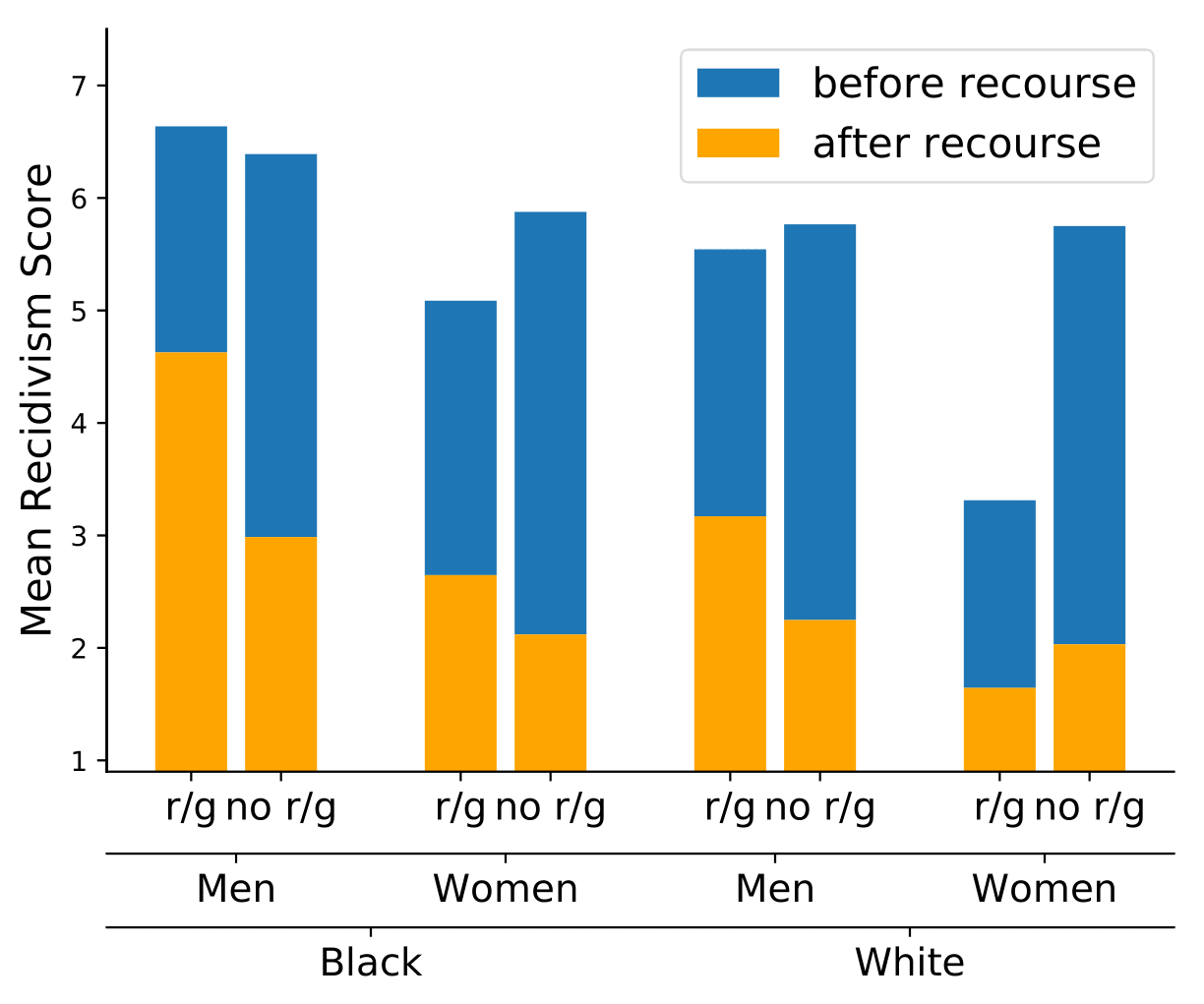
In blue, we see the average COMPAS score (out of 10, lower is better/less risky) before any action is taken by the individuals to change their features, and in orange we see the average COMPAS score after their actions. The left column in each group is the result on a model that uses race and gender in decisions, and on the right is a model that does not. The models were approximately equally accurate, and make similar decisions, as there are many redundant correlations in the data.

However, we can clearly see that when race and gender, immutable characteristics, are excluded from the used features, the agency of individuals increases. Moreover, this is most dramatic for those groups most discriminated against in the criminal justice system (black men). The reason for this is straightforward: when a decision-making function can no longer rely on immutable characteristics in its decisions it relies more heavily on mutable characteristics, which individuals have the power to change. This provides us a new, additional angle for fairness in machine learning: how our choice of features in machine predictions differtly impacts the agency of different groups.

The incentives dictated by decision-making functions may already be causing serious social consequences. We hope our work is another early step to bringing them to light.

-Yo